Resampling - Interpolation
Here we look at converting a signal to a higher sample rate using
interpolation. This process interestingly involves simply 'zero stuffing'
extra samples followed by a low pass filter with cutoff at the OLD
Nyquist frequency. Naturally you are not going to get any wider bandwidth
out of the signal, just change it's sample rate, even though the new
sample rate can accomodate a wider bandwidth signal.
First lets observe the zero padding by setting the filter cutoff
frequency too high:
sampling_freq = 4e6 # original signal at 4Msps
fg = gr.flow_graph ()
src = gr.sig_source_f ( sampling_freq, gr.GR_SIN_WAVE, \
600e3, 1, 0 ) # 600Khz, amplitude 1, 0 offset
# compute low pass filter taps - this time too high cutoff
# to see the zero stuffing
lpf_taps = gr.firdes.low_pass ( \
1.0, # gain
16e6, # new sampling rate, 4X old
8e6, # LPF cutoff at 8Mhz, too high
500e3, # transition band width
gr.firdes.WIN_HAMMING )
interp_filter = gr.interp_fir_filter_fff ( \
4, # interpolation
lpf_taps )
dst1 = gr.file_sink (gr.sizeof_float, "signal_out")
dst2 = gr.file_sink (gr.sizeof_float, "interp_out")
fg.connect (src, dst1) # the original signal
fg.connect (src, interp_filter)
fg.connect (interp_filter, dst2) # upsampled signal
Now lets look at the original signal:
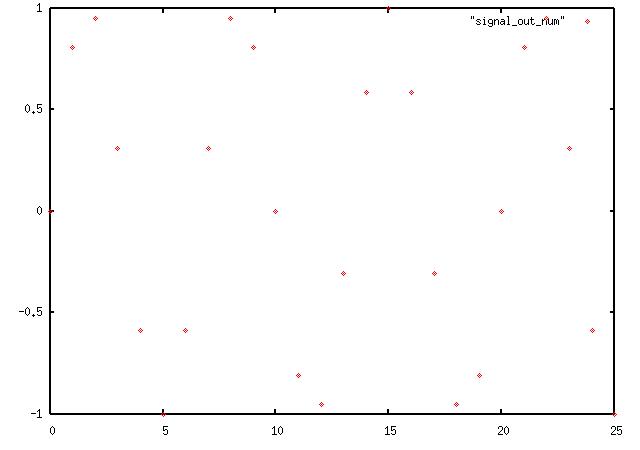
which has about 6.666 points per cycle ( 4Mhz / 600Khz)
Next the upsampled signal with too high filter:

where you can clearly see 3 extra samples at zero between each of the original
signal. Lastly we change the LPF cutoff to recreate the orignal signal at the
new sampling rate. The original signal was sampled at 4Msps so we use 2Mhz:
lpf_taps = gr.firdes.low_pass ( \
1.0, # gain
16e6, # new sampling rate, 4X old
2e6, # LPF cutoff at 2Mhz, just right
500e3, # transition band width
gr.firdes.WIN_HAMMING )
and now you can see we have the original signal at the new sampling rate:
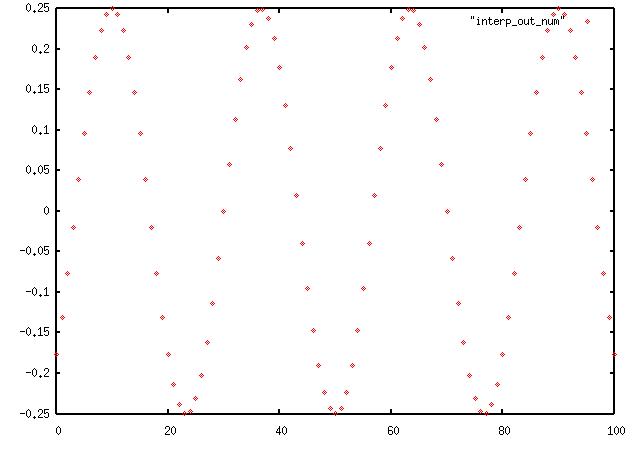
with 26.666 points / cycle ( 16Msps / 600Khz, or 4 * 6.6666 ).


