Pulse shaping and bandlimiting square waves with Root Raised Cosine filters
Here we see how the bandwidth of pulses are limited. I used this before in the psk31 transmitter but then just adjusted parameters for lowest IMD
on a psk31 receiver w/o fully understanding what it was doing.
This experiment clearly shows bandlimiting by adjusting the symbol rate as a function of the sample rate.
We will use a vector source generated square wave with slowly varying duty-cycle
from nearly DC to nearly 0, run it thru a rrc filter and watch it on the fft display with different symbol rates.
The code:
#!/usr/bin/env python
#
#
from gnuradio import gr
from gnuradio import eng_notation
from gnuradio.eng_option import eng_option
from gnuradio.wxgui import stdgui, fftsink
from optparse import OptionParser
import wx, random, math
class app_flow_graph (stdgui.gui_flow_graph):
def __init__(self, frame, panel, vbox, argv):
stdgui.gui_flow_graph.__init__ (self, frame, panel, vbox, argv)
self.frame = frame
self.panel = panel
sample_rate = 50e3
symbol_rate_div = 8
vec = []
for i in range(1,255):
for j in range(0,40):
for k in range(0,i):
vec+=[0]
for k in range(i,256):
vec+=[100]
for i in range(255,1,-1):
for j in range(0,40):
for k in range(0,i):
vec+=[0]
for k in range(i,256):
vec+=[100]
pulse = gr.vector_source_c(vec,1)
rrcf_coeffs = gr.firdes.root_raised_cosine(1.0, sample_rate, sample_rate/symbol_rate_div, .5, 337)
rrcf = gr.fir_filter_ccf(1,rrcf_coeffs)
fft, fft_win = fftsink.make_fft_sink_c (self, panel, "", 256, sample_rate)
self.connect (pulse, rrcf)
self.connect (rrcf, fft)
vbox.Add (fft_win, 1, wx.EXPAND)
def main ():
app = stdgui.stdapp (app_flow_graph, "USRP FFT")
app.MainLoop ()
if __name__ == '__main__':
main ()
Results:
Using symbol_rate_div = 1 (symbol rate equals sample rate) and a sample rate
of 50Khz we see the signal uses all available bandwidth, -25 to +25Khz:

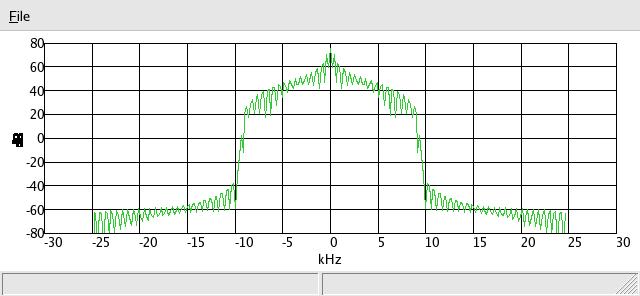
If we change the symbol rate to half the sample rate, we get this:
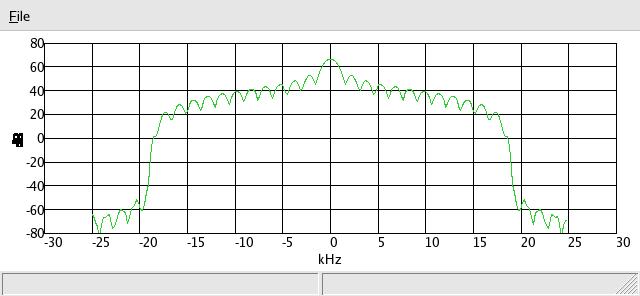
One forth the sample rate:
Time domain plot of the above:
One sixth the sample rate:
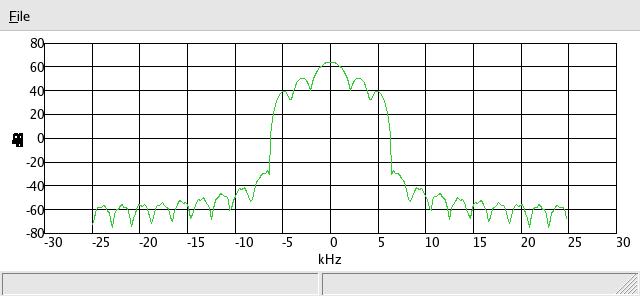
lastly one eighth:
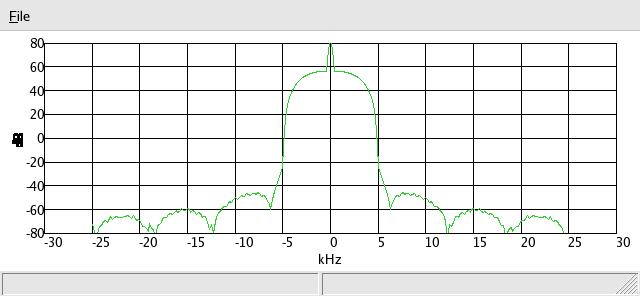
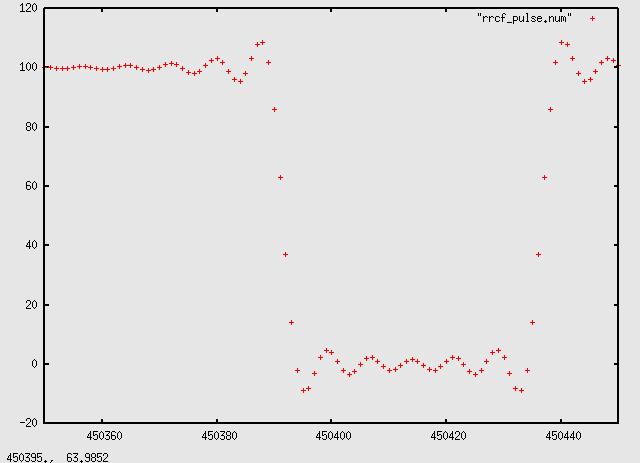
and the time domain signal of symbol rate = 1/8th sample rate:







