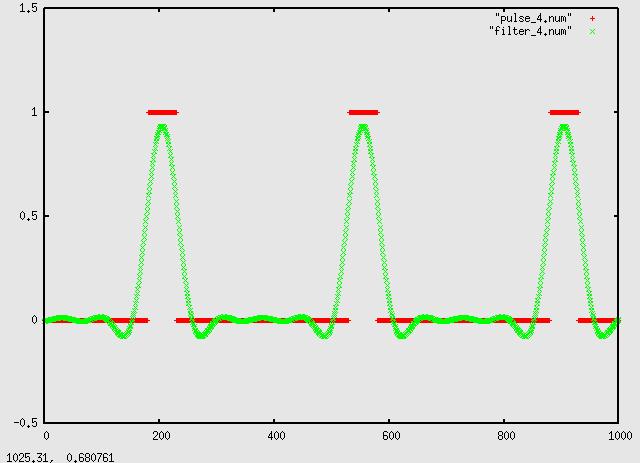
Pulse shaping and adding after low pass filtering
For some time I've been wanting to understand and create a function like this:

where a series of pulses (or bands of frequencies) are bandlimited and combined yet retain enough just enough information to remain distinct - the point being
that the peak of each pulse occurs in it's sinc function where the sinc function
of the other pulses are zeros. This is to prevent ISI, inter-symbol-interference. As you can see, the green plot peaks, and is a valid
sample of the pulse amplitude, exactly where the purple and brown plots cross zero.
Some math: Working from Stremler, we are told (in a discussion of Pulse Amplitude Modulation) that "the absolute
minimum bandwidth required such that the information in each sampled channel remains independent of that in the other channels" (Forget the multiple channels
for now, we just want each pulse to remain independent from the rest) requires
a low-pass filter with bandwidth greater or equal to 1/(2T) where T is the time
between INDIVIDUAL pulses (not pulse cycle time, etc. That is, one cycle of a square wave is two pulses).
To test this the following code uses 1Mhz sample rate, and pulses of 50 samples, giving a T of 50uSec, so our low pass filter must have at least 1/(2*50us) or 10Khz bandwidth. I also create a vector of 7 pulses, each one of which can
be individually turned on and off to get their separate and combined influence on the output. The above plot was created with the vector [0,0,5,5,5,0,0] and
making seperate runs with src3,4,5 on and plotting the results. With src3,4,5
all on at the same time we get the summation:

#!/usr/bin/env python
#
#
from gnuradio import gr
from gnuradio import audio
import sys
import math
def build_graph ():
fg = gr.flow_graph ()
sample_rate = 1e6
vec0 = [0,0,0,0,0,0,0]
sig1 = [0,0,0,0,0,0,0]
vec1 = []
for i in range(0,len(sig1)):
a=sig1[i]
for j in range(0,50):
vec1+=[a]
sig2 = [0,0,0,0,0,0,0]
vec2 = []
for i in range(0,len(sig2)):
a=sig2[i]
for j in range(0,50):
vec2+=[a]
sig3 = [0,0,5,0,0,0,0]
vec3 = []
for i in range(0,len(sig3)):
a=sig3[i]
for j in range(0,50):
vec3+=[a]
sig4 = [0,0,0,5,0,0,0]
vec4 = []
for i in range(0,len(sig4)):
a=sig4[i]
for j in range(0,50):
vec4+=[a]
sig5 = [0,0,0,0,5,0,0]
vec5 = []
for i in range(0,len(sig5)):
a=sig5[i]
for j in range(0,50):
vec5+=[a]
sig6 = [0,0,0,0,0,0,0]
vec6 = []
for i in range(0,len(sig6)):
a=sig6[i]
for j in range(0,50):
vec6+=[a]
sig7 = [0,0,0,0,0,0,0]
vec7 = []
for i in range(0,len(sig7)):
a=sig7[i]
for j in range(0,50):
vec7+=[a]
src0 = gr.vector_source_f(vec0, 1)
src1 = gr.vector_source_f(vec1, 1)
src2 = gr.vector_source_f(vec2, 1)
src3 = gr.vector_source_f(vec3, 1)
src4 = gr.vector_source_f(vec4, 1)
src5 = gr.vector_source_f(vec5, 1)
src6 = gr.vector_source_f(vec6, 1)
src7 = gr.vector_source_f(vec7, 1)
filter_coeffs = gr.firdes.low_pass ( 1.15, sample_rate, 10e3, 1e3, gr.firdes.WIN_HAMMING )
print "filter length",len(filter_coeffs)
filter1 = gr.fir_filter_fff ( 1, filter_coeffs )
filter2 = gr.fir_filter_fff ( 1, filter_coeffs )
filter3 = gr.fir_filter_fff ( 1, filter_coeffs )
filter4 = gr.fir_filter_fff ( 1, filter_coeffs )
filter5 = gr.fir_filter_fff ( 1, filter_coeffs )
filter6 = gr.fir_filter_fff ( 1, filter_coeffs )
filter7 = gr.fir_filter_fff ( 1, filter_coeffs )
add_pulses = gr.add_ff ()
add_filtered = gr.add_ff ()
pulse_out = gr.file_sink(gr.sizeof_float, "pulse")
filter_out = gr.file_sink(gr.sizeof_float, "filter")
fg.connect ( src0, (add_pulses, 0) )
fg.connect ( src0, (add_pulses, 1) )
fg.connect ( src3, (add_pulses, 2) )
fg.connect ( src4, (add_pulses, 3) )
fg.connect ( src5, (add_pulses, 4) )
fg.connect ( src0, (add_pulses, 5) )
fg.connect ( src0, (add_pulses, 6) )
fg.connect ( add_pulses, pulse_out )
fg.connect ( src0, filter1, (add_filtered,0) )
fg.connect ( src0, filter2, (add_filtered,1) )
fg.connect ( src3, filter3, (add_filtered,2) )
fg.connect ( src4, filter4, (add_filtered,3) )
fg.connect ( src5, filter5, (add_filtered,4) )
fg.connect ( src0, filter6, (add_filtered,5) )
fg.connect ( src0, filter7, (add_filtered,6) )
fg.connect (add_filtered, filter_out)
return fg
def main ():
fg = build_graph()
fg.start()
raw_input ('Press Enter to quit')
fg.stop()
if __name__ == '__main__':
main ()
Here are some more except using the root_raised_cosine filter instead
of low_pass.
filter_coeffs = gr.firdes.root_raised_cosine ( 1, sample_rate, sample_rate/50, .05, 180 )
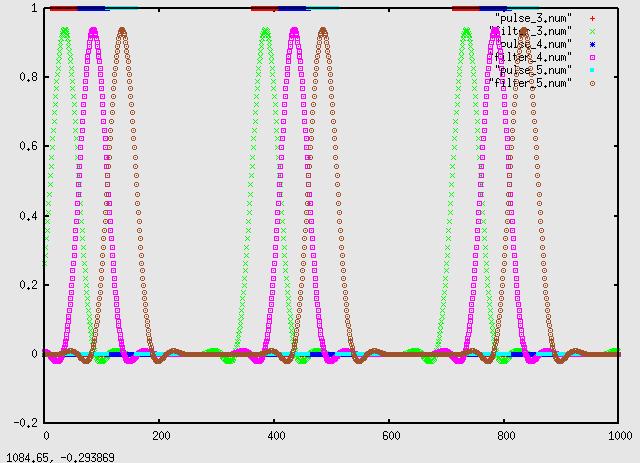
Seperate pulses, and alpha=.5:

Combined pulses, alpha=.5:
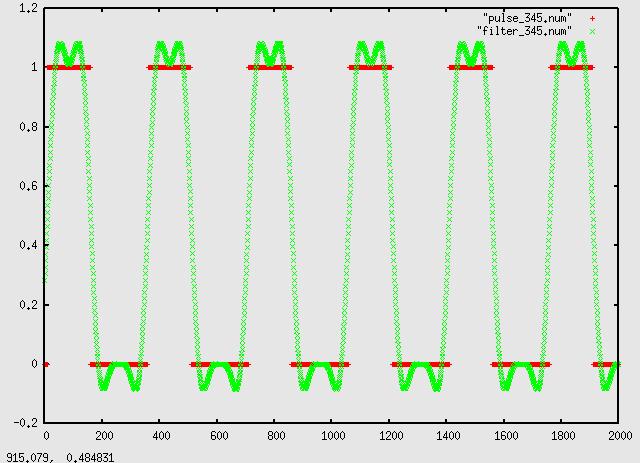
Alpha=.95, seperately:
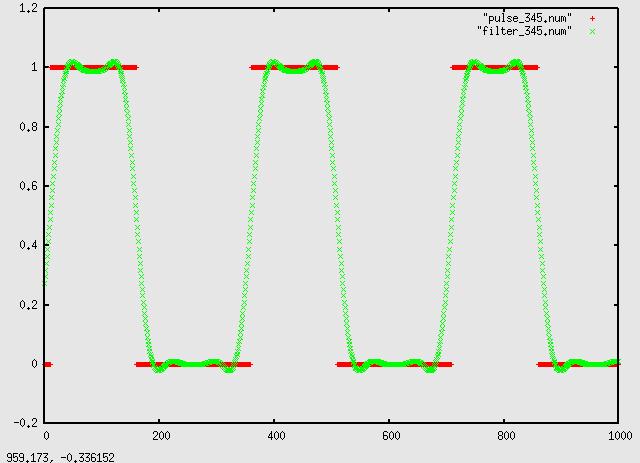
combined:
Alpha=.05, seperately:
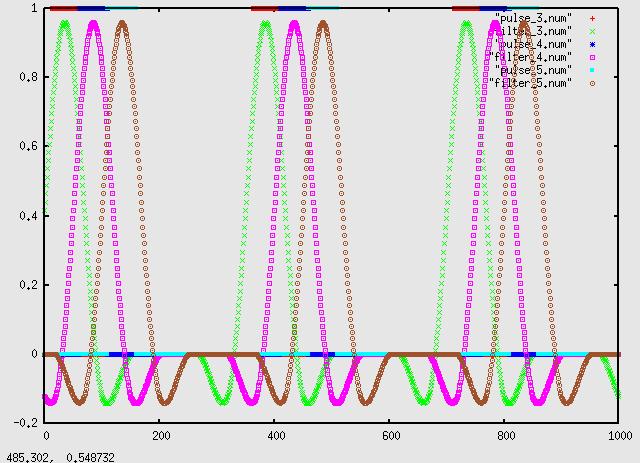
and combined:

Playing with the number of taps in the rrcf, alpha=.5, here's 40:

80 taps:
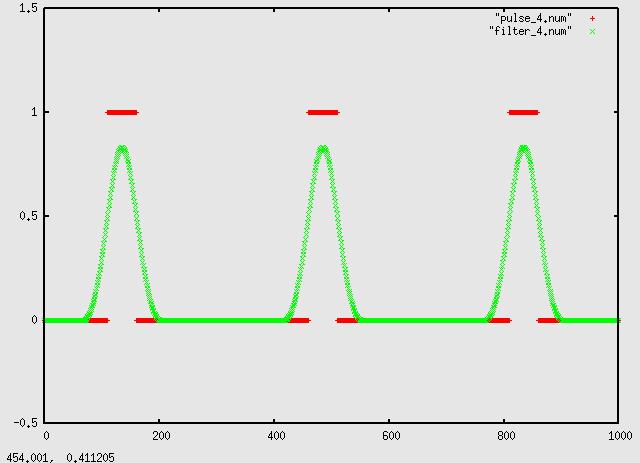
160:
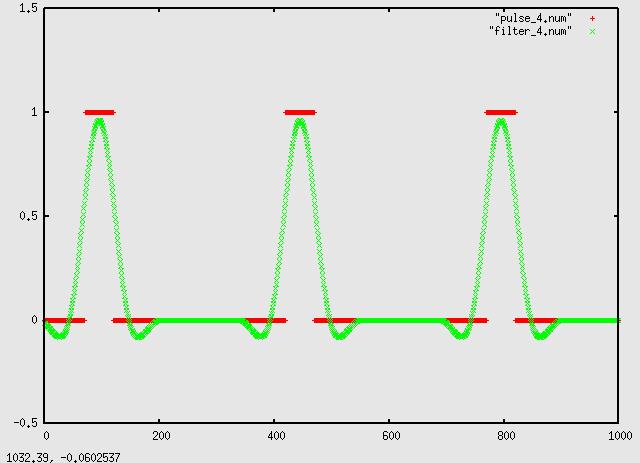
320:
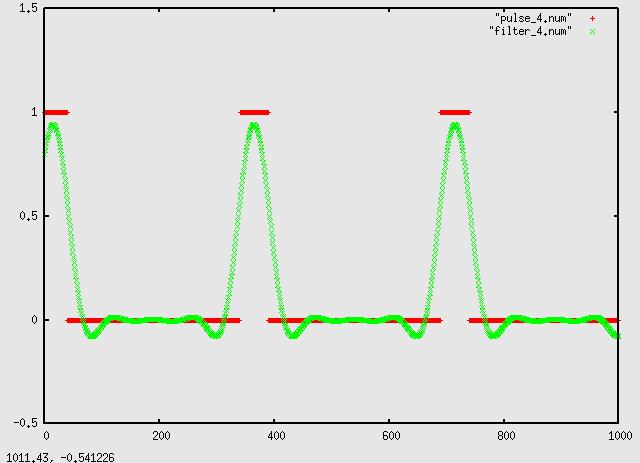
and 640 taps: