Notch Filter
An audio notch filter can be created based on the following example: to remove a
signal of 1Khz, you delay the signal by 1/2 cycle and add back to the original.
For a 1Khz tone the required delay would be 1/2 a millisecond. We can calculate
the delays for other frequencies to notch out. For a sampling rate of 32000,
a fir filter delays by 31.25 uSec per stage. To calculate every possible
notch frequency for this delay, we can use the following python script:
unit_delay = ( 1 / 32000.0 )
for delay in range(1,100):
print delay, ( 1 / ( delay * unit_delay ) ) / 2
which give us this list of number of delay stages
and what freq gets notched. A partial list:
16 1000.0
17 941.176470588
18 888.888888889
19 842.105263158
20 800.0
So for a notch freq of 1000 Hz, we need 16 delay stages at 31.25 uSec per
stage, which is the delay at 32,000 Samples / second.
The following script implements a 1Khz notch filter:
notch_3.py
sampling_freq = 32000
fg - gr.flow_graph ()
# notch filter frequency = ( 1 / ( delays * unit_delay ) /2
# where unit_delay = 31.25 uSet for 32000 sampling rate
# in the following we use 16 delays for a notch of 1Khz
taps = [1] # original signal, no delay
for i in range(1,16):
taps = taps + [0]
taps = taps + [1] # delayed signal
src0 = gr.sig_source_f (sampling_freq, gr.GR_SIN_WAVE, 1000, 1)
# simply delay for 16 * 31.25 uSec, .5 mSec, then add back
# to original signal
notch = gr.fir_filter_fff (1, taps)
dst = gr. file_sink (gr.sizeof_float, "notch.out")
fg.connect (src0, notch)
fg.connect (notch, dst)
That gives us this frequency response:
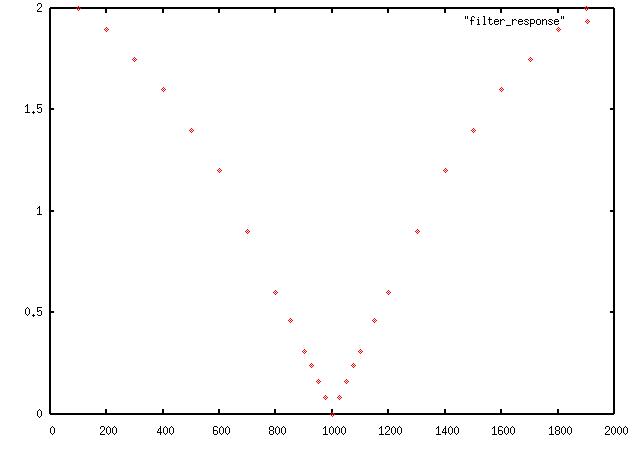
Note that unfiltered signals far from the notch are doubled, essentially
added to itself, while the notch is down to zero.
It turns out that the above notch filter is actually a comb filter with 16
notches between 0 and the sample rate. The shifting by 1/2 cycle and adding
not only filters the fundamental frequency, but all odd harmonics. The
equation for a feed-forward comb filter (which only requires a fir filter,
the current output only depends on previous input, NOT previous outputs) is:
y[n] = ax[n] + bx[n-M]
which is implemented just as above with gr.fir_filter_fff( 1, [1, 0, 0, ... 0, 0, 1]) - that is, a=b=1, and add the current input with the input 16 samples ago.
Here is a similar filter as above, except using 48Khz sample rate and 24 delay taps, applied to a noise source:
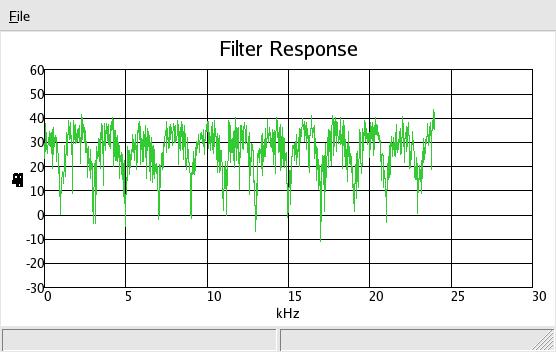
where you can see the nulls at 1,3,5,7,9,11Khz etc and up. Using smaller values for
'b' results in less deep nulls.

