Forward & Inverse DFT

Here we take the discreet Fourier transform of a sine wave and a square wave, the immediately take the inverse DFT and look at the results.

Test code:

#!/usr/bin/env python
#
# 

from gnuradio import gr
import sys
import math

def build_graph ():

	fg = gr.flow_graph ()
	sample_rate = 32000
	fft_size = 256

	vec = []
	for j in range(0,7):
	  for k in range(0,3):
	    vec += [1+1j]
	  for k in range(4,7):
	    vec += [0+0j]

	src = gr.vector_source_c(vec, 1)
#	src = gr.sig_source_c (sample_rate,gr.GR_SIN_WAVE,440,1,0)
	s2p = gr.serial_to_parallel (gr.sizeof_gr_complex, fft_size)
	fft1 = gr.fft_vcc (fft_size,True,False)   # forward=True
	fft2 = gr.fft_vcc (fft_size,False,False)  # forward=False
	p2s_2 = gr.parallel_to_serial (gr.sizeof_gr_complex, fft_size)
	dst = gr.file_sink (gr.sizeof_gr_complex, "fft_ifft")

	p2s_1 = gr.parallel_to_serial (gr.sizeof_gr_complex, fft_size)
	fft_1 = gr.file_sink(gr.sizeof_gr_complex, "fft")

	fg.connect ( src, s2p )
	fg.connect ( s2p, fft1 )
	fg.connect ( fft1, fft2 )
	fg.connect ( fft2, p2s_2 )
	fg.connect ( p2s_2, dst )

	fg.connect ( fft1, p2s_1 )
	fg.connect ( p2s_1, fft_1 )

	return fg

def main ():
	fg = build_graph()
	fg.start()
	raw_input ('Press Enter to quit')
	fg.stop()

if __name__ == '__main__':
	main ()

where we choose sig_source or vector_source for sin or square waves. First, the plot of the transform of the sine wave:

Now if we take the inverse dft of the above transform we get:

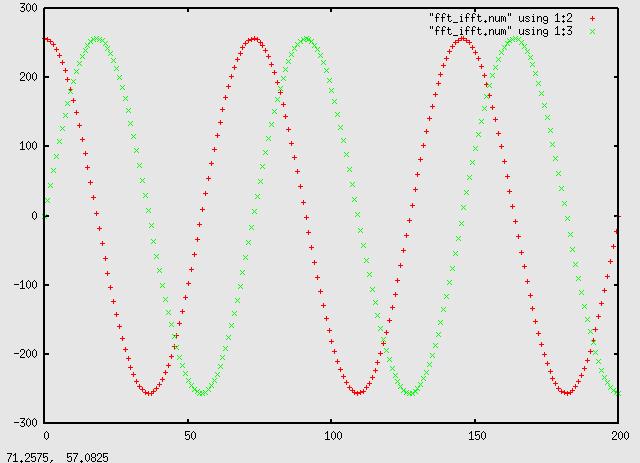
which, amazingly, nicely recreates the original signal ok except for the amplitude.

Next, the transform of a square wave:

and the inverse transform of it:

Finally the dft transform of an impulse:

a closer look:

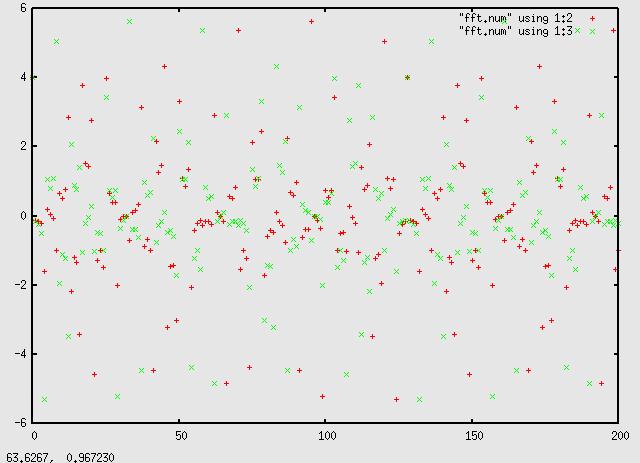
and here's the reverse dft of the above

which gets our original impulse back, except for the magnitude.