0 DC Restorer

In demodulating AM signals we end up with the problem of a DC offset bias on the resulting demodulated information. A simple differentiator

	y[n] = x[n] - x[n-1]

removes the DC but also attenuates lower frequency signals. A FIR filter with one delay can give us a differentiator. From what I could find the consensus is to follow the differentiator with a 'leaky' integrator

	y[n] = .999 * y[n-1]  + x[n]

Since this requires past outputs ( y[n-1] ) to calculate the current output (as opposed to past inputs for the differentiator) we have to use an Infinite Impulse Response filter. In the following we just use '1' for '.999' which works in many cases.

0dc_restorer.py

#!/usr/bin/env python
#
# Copyright 2004 Free Software Foundation, Inc.
# 
# This file is part of GNU Radio
# 
# GNU Radio is free software; you can redistribute it and/or modify
# it under the terms of the GNU General Public License as published by
# the Free Software Foundation; either version 2, or (at your option)
# any later version.
# 
# GNU Radio is distributed in the hope that it will be useful,
# but WITHOUT ANY WARRANTY; without even the implied warranty of
# MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
# GNU General Public License for more details.
# 
# You should have received a copy of the GNU General Public License
# along with GNU Radio; see the file COPYING.  If not, write to
# the Free Software Foundation, Inc., 59 Temple Place - Suite 330,
# Boston, MA 02111-1307, USA.
# 

from gnuradio import gr

def build_graph ():

	sampling_freq = 8e6

	fg = gr.flow_graph ()

	src = gr.sig_source_f (
		sampling_freq,
		gr.GR_SIN_WAVE, .455e6,
		1.5, -2.38)


	diff = gr.fir_filter_fff ( 1, [1, -1] )
	int = gr.iir_filter_ffd ( [1, 0], [0, 1] )

	dst_i = gr.file_sink (gr.sizeof_float, "restore_in")
	dst_o = gr.file_sink (gr.sizeof_float, "restore_out")

	fg.connect (src, dst_i)
	fg.connect (src, diff)
	fg.connect (diff, int )
	fg.connect (int, dst_o)

	return fg

def main ():
	fg = build_graph()
	fg.start()
	raw_input ('Press Enter to quit')
	fg.stop()

if __name__ == '__main__':
	main ()

produces the following output:

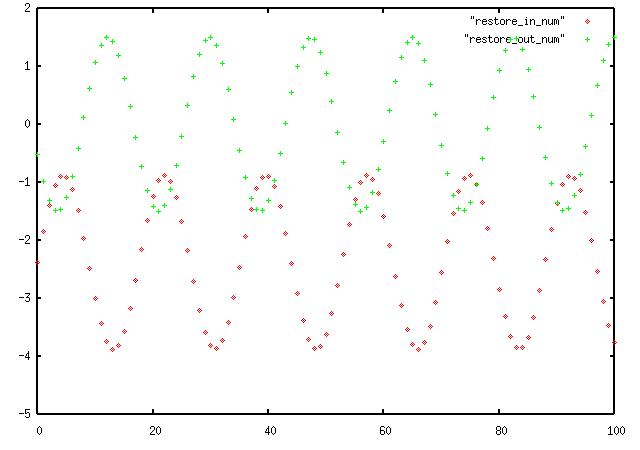
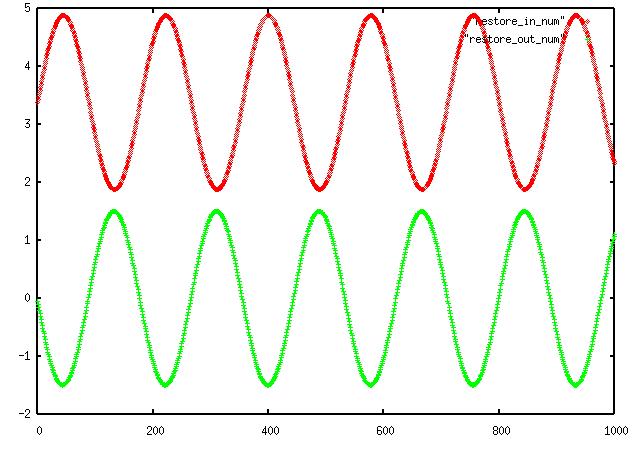
Notice the 180 degree phase shift, the red is the offset input and the green output is nicely centered about zero. Next we try a different frequency and offset, but leave the amplitude of the test signal the same to make sure the output amplitude is not frequency dependant:

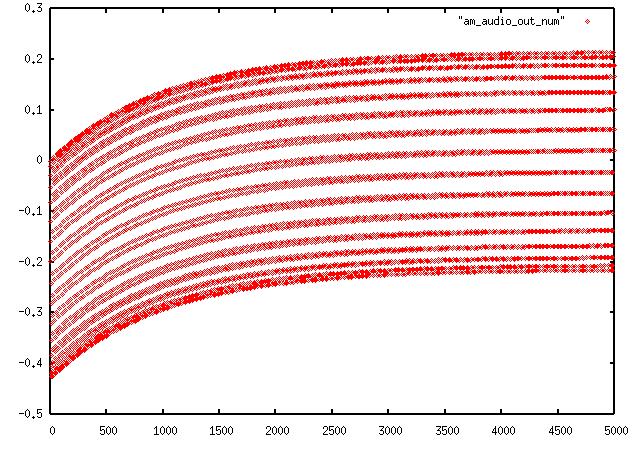
While the above works for many tests cases, the need for the 'leaky' part just came up in another application, where we must use:

	diff = gr.fir_filter_fff ( 1, [1, -1] )
	int = gr.iir_filter_ffd ( [1, 0], [0, .999] )

using a 'close to 1' number. The difference between .99 and .999 is illustrated in these two plots - my signal was staying in negative territory untill changing the '1' to 'close to 1'. First with .999:

and the next with .99: