Experiment #5: series RLC circuit

This verification experiment uses the 1nF capacitor and the 1.5uH inductor connected in series with a 51 ohm resistor to the VNA on a breadboard and the 6" piece of RG-174. I use the same calibration data files from experiment #1. Then I run f_sweep_tr.py stopping at 10Mhz. This creates a data file RLC_series_refl_raw. This is compensated with

	$ ./refl_calc_1.py calib_refl_open calib_refl_short calib_refl_load RLC_series_refl_raw RLC_series_refl_comp

and then display the results by converting from polar to rectangular form with

	$ ./convert_rpt_to_smith3.py RLC_series_refl_comp RLC_series_refl_comp_smith

then putting the filename into smith_chart and plotting with gnuplot: $ gnuplot smith_chart

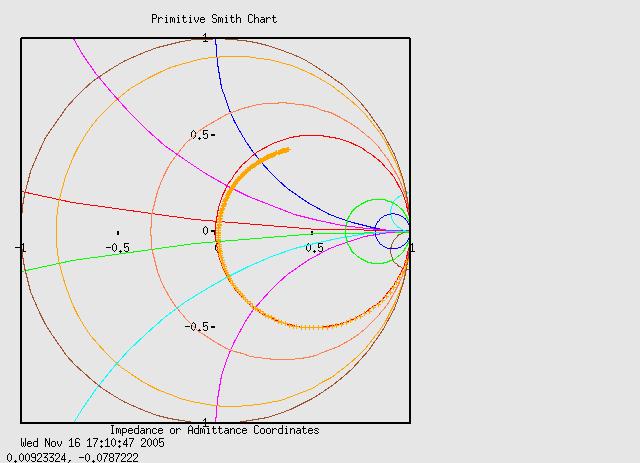
A series resonant RLC circuit appears as a low impedance where inductive reactance equals capacitive reactance. This time at resonance the 51 ohm resistor makes a near perfect match to the 50 ohm transmission line and reflection is near zero, at the center of the graph, at about 4.15MHz. Interestingly the curve follows the normalized R=1 (or R=50 un-normalized) circle. Also, I've noticed in many test runs that an inductors resistance increases at higher frequencies. That explains the turning in from the R=1 circle near the top. However I cannot explain why the appearant resistance increases in an inductor. Skin effect? At 1MHz, R=48.76 and slowly increases to 51.37 ohm at f=4.15MHz - it is a 51 ohm resistor (5%). However at 9.9MHz R increases to 59.34 ohms. Look at the value of R in experiment #1 (the 1.5uH inductor) - it is 8.45 ohms at 10MHz, and only 1.5 ohms at 4.15MHz, and 0.129 ohms at 1Mhz.